依托几何直观 培养数学素养
钟丽娟


摘要:几何直观就是依托、利用图形进行数学地思考和想象。德国数学家希尔伯特专门写了一本专著叫《直观几何》。法国数学家笛卡尔发明了数轴,巧妙地将数与形结合在一起……这说明几何直观在学习数学中的作用是非常大的,可以培养小学生的多方面的数学素养。
关键词:几何;数学;基础教育
中图分类号:G623.5 文献标志码:A 文章编号:1674-9324(2018)44-0203-02
《义务教育数学课程标准(2011年版)》(以下称《标准》)明确指出,几何直观可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用。那么依托几何直观,小学生数学学习应该真正培养哪些方面的数学素养呢?
一、依托几何直观,发现数学问题
《标准》在总目标中明确提出要“增强发现和提出问题的能力、分析和解决问题的能力”。但在实际教学中,我们发现学生的“发现和提出问题的能力”较弱,表现为小学生难以把生活中的数学现象转化成数学问题,难以把数量或空间方面的某些关系转化成数学问题。
例如,人教版五年级下册“分数的意义”一课,可以这样设计:①观察:把一张纸条对折,再对折,其中的一折用一个数怎么表示?你是怎么理解的?②思考:还能用其他的方式来表示吗?(温馨提示:画、摆、涂、折等);有的学生说“把一个圆四等分,每一份用”;有的学生说有四枚一元硬币,其中一枚占;有的学生说“一张《小学生周报》有四版,我看完第一版,看了”……③讨论:这些活动有什么共性?有的学生说“它们都进行了等分”;有的学生说“它们都表示其中一份,所以都用表示”。④质疑:你发现什么问题吗?有的学生质疑说“虽然这些例子是用表示,但表示的是不同东西的,有的是一个,有的是几个组成的,表示的大、小、多、少都不一样”。有的学生进一步提出“其他的分数也能这样表示吗?”等。
二、依托几何直观,描述数学现象
几何直观描述数学现象,既是发展学生空间观念的重要途径,也是培养学生数形结合思想的重要抓手。例如,在教学“正比例的意义”一课时,学生对形如①y=2x中,x和y成正比例比较容易理解。而对于形如②x和③中x和y成正比例就感到难以理解。这是因为正反比例描述的是两个变量之间的关系,概念本身比较抽象。再加上后两式属于①式的变式题,在缺乏直观帮助下大部分学生难以接受后两种变式x和y也成正比例。要扫清思维障碍,建立“成正比例关系”的思维图式,可采用先列表再画图的描述方法加以解决。
经过列表法观察,可以发现不管形式怎么变化,变量y和x的比值也就是商是一定的,所以这两种量成正比例关系。
图像法:
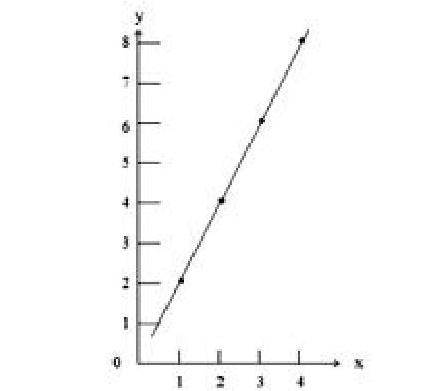
上述三个表格的内容实际上是一样的。如果把上述表格图成图像,则可用下图表示:
当上述三个变式采用图像描述时,学生惊奇地发现这三个式子实际表示的都是同一个图像,即一条向两端无限延伸的直线!通过用表格进行列举,再用图像加以描述,学生在头脑里建立起成正比例关系的心理图式,这其实就是数学的本质。这种从代数关系式描述到列表法描述再到图像描述之建立起一一对应的关系,充分体现了数形结合的思想。
三、依托几何直观,外化数学思考
培养学生以数学的眼光看世界,从数学的角度去分析问题的素养,会使学生终生受益,而无论他们将来从事什么职业,这是一种用“数学方式进行的理性思维”。
例如,学校举行乒乓球社团小组争霸赛。五年级社团有10个选手,每两人进行一场争霸赛,一共要进行几场争霸赛?
生1:可以这样想,第一个小运动员要和其他9人各打1场,共9场;第二个小运动员要打8场,第三个小运动员要打7场,……最后一个小运动员只打1场就够了。因此列式是9+8+7+6+5+4+3+2+1=(9+1)+(8+2)+(7+3)+(6+4)+5=45(场)。
生2:其实不用那么复杂,可以看成数线段,用连线的方法解决。10个运动员相当于10个点,每两个点可以连成一条线段。第一个点可以边9条,第二个点可以连8条,以后每次少1条,依此类推。9+8+7+6+5+4+3+2+1=45(条),也就是45场。
生3:我也是用数线段的方法来解决,可是我画的线段和他不一样,答案也是45场。
生4:从1一直加到9,后一个数都比前一个数多1。我觉得可以看成一个梯形,用数木头的方法来解决。即(顶层根数+底层根数数)×层数÷2,也就是(1+9)×9÷2=45(根),也就是45场。从直接用等差数列求和的方法解,到用数线段连线的方法,再到看成堆成一垛木头,用梯形面积计算公式来计算。
四、依托几何直观,预测数学结果
有些数学研究的对象是可触的、可视的、具象的,而很多数学研究对象是“看不见,摸不着”的,是抽象的、内隐的,这是数学的一个基本特点,也给小学生解决问题带来相当大的困难。例如,一张桌子坐8人,两张桌子并起来坐12人,三张桌子并起来坐16人,照这样计算,六张桌子并成一排可以坐多少人?(如图所示)
因为只有六张桌子,所以大部分的学生轻松地获得结果。学生们通过画图:一张、两张、三张……一共可以坐28人。表面上學生通过画图解决问题的思维含量不高,其实不然,关键取决于老师是否能基于核心素养来定位我们的教学。如果老师这样教学:同学们,假如有20张这样的桌子并排,可以坐几个人?再用画图的方法合适吗?你能从刚才六张桌子的图中发现什么规律?学生通过认真观察、讨论,不难发现“桌子头尾4个人始终固定不变的,而两侧每增加一张桌子就增加4个人”这一重要的规律。这时,老师不失时机地点拨:如果有n张桌子,这样并排,你能用一个含有字母的式子表示所坐的人数吗?学生学会用(4n+4)来表示人数。此时老师再进一步提出现在有28人,按照这样子坐法,一共要并排几张桌子?从画图计算人数,到观察图形的规律,再到抽象出含有字母的式子表示人数,再进一步解决逆思考题,学生借助几何直观,完成了数学抽象和思维的互逆训练。借助几何直观学生不但学会了画图预测结果,还在找规律的过程中体验了数学抽象、推理、建模等基本思想。
华罗庚教授曾说“形缺数时难入微,数缺形时少直观”。要更好地研究数学,离开了图形是不可想象的。只要我们做个有心人,帮助学生建立起实物与概念、图形与概念间的联系,化抽象为具象,变内隐为外显,就可以促使学生更好地理解数量之间和空间形式的本质,也能够提高学生学习的兴趣。
Abstract:Geometric intuitionism is relying on figure to think and imagine mathematically. German mathematician Hilbert wrote a monograph called intuitive Geometry. The French mathematician Descartes invented the number axis. It shows that geometry intuitionism plays a very important role in learning mathematics,and it can cultivate pupils' mathematics literacy in many aspects.
Key words:geometry;mathematics;basic education
- 上一篇:吴井生,杨剑波,张建生,邢军——录用通知书(jyjxlt@j 2019/3/11
- 下一篇:吴井生,杨剑波,张建生,邢军——录用通知书(jyjxlt@j 2019/3/11
