[出处] 教育教学论坛_2022年第25期

陈菁菁 金美含 罗钦

[关键词] 应用数学;硕士研究生教学;专业应用;PDCA循环

[基金项目] 2019年度广东省教育厅广东省本科高校教学质量与教学改革工程建设项目“‘交通运输’特色专业”;2021年度深圳技术大学研究生课程教学案例项目“应用数学”（20213108080002）

[作者简介] 陈菁菁（1977—），女，湖南新宁人，博士，深圳技术大学城市交通与物流学院教授，主要从事交通运输规划与管理、应用数学教学研究;金美含（1988—），女（朝鲜族），吉林省吉林市人，博士，深圳技术大学城市交通与物流学院教授，主要从事时空大数据挖掘、应用数学教学研究;罗 钦（1982—），男，湖南浏阳人，博士，深圳技术大学城市交通与物流学院教授，主要从事轨道交通运营组织管理研究。

[中图分类号] G643 [文献标识码] A [文章编号] 1674-9324（2022）25-0132-04 [收稿日期] 2022-03-14

科技需要数学的支撑，计算机、控制论、信息论、计算数学、博弈论等具有强大生命力的数学分支都是新技术的坚实基础。数学应用与行业发展相辅相成。数学是工程实践的重要基础，是研究生必备的基础知识。利用数学工具解决工程问题的能力是工科研究生能力培养中非常重要的目标。一方面，传统的数学教学偏重理论推导，缺少数学在工程中的应用，特别缺乏专业针对性强的应用;另一方面，技术和行业的发展，对数学应用能力提出了新的要求，需要加强数学教学内容与工程实际需求的紧密结合。

一、基于专业应用构建数学知识框架

数学是研究数量、结构、变化、空间及信息等概念的一门学科，其分支庞大，内容深奥，应用广泛，在数学教学中不可能面面俱到。而不同专业研究生的研究领域差异明显，对数学知识的学习需求也存在差异。在数学知识内容选择上，教师应分析专业领域的核心理论和发展趋势，突出关键应用，有重点有选择地讲授数学理论知识。同时，关注专业发展中新研究范式的变化对数学知识的更新和补充，为学生构建与本专业或研究方向相关性强的数学知识框架，为今后的研究工作开展奠定有效的基础。

（一）选择面向专业应用的数学知识点

教师可以根据专业需求对数学能力的要求，来选择教学内容知识点。以交通运输专业为例，该专业方向的研究生主要以交通系统为研究对象，面向由千万级个体出行需求与多种交通方式供给构成的复合网络，研究其构建和运行的相關问题。

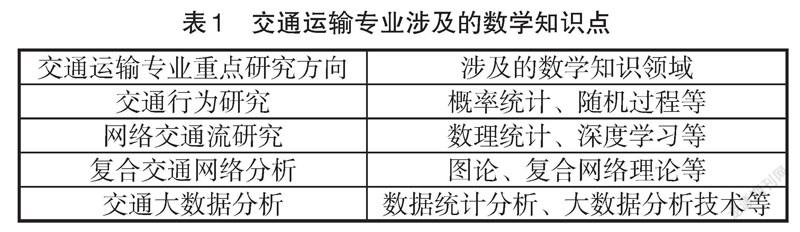
在面向交通运输专业研究生的应用数学课程中，除了常规概率统计、运筹学等基础数学知识点外，根据交通行业发展和研究新范式的引入，增加复杂网络理论和大数据分析方法等针对性强的知识点。交通运输专业涉及的教学知识点如表1所示。

（二）梳理关键数学知识点的应用体系

当知识点以一种层次网络结构的方式进行储存时，可以大大提高知识应用时的检索效率。教师针对关键知识点，以专业应用为导向，建立该知识点的结构，帮助学生将碎片化的知识点加以归纳和整理，按层次排列，使之条理化、纲领化，做到纲举目张。教师通过数学原理讲解和专业应用案例分析，比较不同数学方法的差异，特别是针对实际问题时不同数学方法应用的优势和局限性。

以交通出行预测应用为例，对于交通运输专业研究生而言，交通出行预测是该研究领域的基础，数学模型是出行预测的重要手段。在教学过程中，一方面，从数学原理层面讲解各类预测模型的基本原理、发展趋势、模型改进方向等;另一方面，结合该专业应用的不同细分领域，梳理出数学模型的应用体系[1]，引导学生构建数学知识与专业应用的联系。

二、基于案例教学设计数学思维能力训练

在研究生进入独立研究阶段，往往会出现遇到问题找不到解决思路，知道数学原理却无法有效与专业研究进行对应的问题。研究生的“应用数学”课程具有理论与应用的双重属性，比较适合作为学生思维能力训练载体，且以专业为单元的教学规模、小班化教学，具备开展思维训练的可行性。

通过案例教学将知识讲授、思维训练融为一体，是培养学生数学抽象思维和解析实际问题能力的有益尝试[2]。教师可以利用案例式教学法，以专业研究的热点和难点为切入点，结合专业实际问题特点，针对主要知识点模块，收集典型案例，重点讲授数学应用思想和科学分析方法在专业领域的应用。教师可以设计循序渐进的课堂讨论和头脑风暴环节，聚焦某一个问题展开深入讨论，包括实际问题与数学模型的差异性讨论、数学假设的合理性讨论、数学解析的局限性讨论、实际问题的复杂性讨论等。

（一）对现实问题的抽象分析能力

抽象能力就是在思维活动中，通过对事物整体性的科学分析，从复杂问题中剖析出问题的主线和主要因素，将问题一般化，以分析、综合、比较为基础，为判断和推理提供前提条件，是实际问题转化为数学模型或数学分析的关键，也是工科研究生开展研究工作的必备素质。

教学过程中，教师可以以专业实践中的案例为切入点，聚焦学生发现问题、提出问题、分析问题、解决问题能力的训练。可以遵循以下步骤来开展课堂教学工作：（1）教师选择行业热点研究问题，抛出该问题的现象，通过课题互动讨论，启发学生思考，并共同总结问题的核心，特别要注意问题的边界条件。（2）聚焦某一核心问题进行分析，采用5W1H框架（如表2）分析问题要素，定位问题方向和关键要素。（3）引导学生尝试将具象问题抽象为一般问题，再选择数学方法，鼓励学生提出不同的方法选择，并对比不同学生在这个过程中的思考，学生间互相启发，有助于提升学生的积极性，也可以从中发现学生个体思维差异。

（二）構建专业逻辑与数学逻辑的关联

研究生的培养更加注重学生在专业领域的深度研究能力，而数学能力是研究能力向纵深发展的坚实基础。但他们往往无法将数学逻辑与专业逻辑进行深度融合，影响了数学方法应用的有效性。在教学过程，针对现实问题，通过问题剖析和数学方法的运用，把一个现实问题抽象为数学可以解析的问题，并进行求解，得到经数学分析得出的结论。同时，需要把这个结论还原到现实问题中，解释现实问题，转化为决策能力，进而提升解决问题的能力。

在课堂上，教师和学生通过专业或行业热点问题相关案例剖析讨论，针对案例的应用场景，启发学生建立专业逻辑与数学逻辑的关联。一方面，可以围绕某一个数学理论或原理，选取专业相关的多个实例，让学生从不同的角度理解某一个理论原理的多维度应用。比如，复杂网络理论可以应用于交通网络分析，这一理论既可以针对静态交通网络的结构特征进行研究，也可以针对动态交通网络的可达性进行研究。另一方面，从某一个专业的典型案例出发，将多个数学理论原理串联起来，让学生理解数学应用的交叉性和复杂性，比如关于交通设施设备管理优化，既会涉及运筹优化模型，又会涉及大数据分析方法。

（三）贯穿系统性思维

对于研究生而言，不论是探索性研究，还是宏观态势研究和微观机理研究，系统性思维能力的培养尤为重要。在对数学知识点的针对性、局限性、关联性有较为全面认知的基础上，启发学生在宏观上思考其在整个数学理论中的作用以及与其他理论之间的联系，在微观上思考其概念本身的深度，其具有的特点、满足的性质及发展的趋势等，这些是构建学生系统性思维的有效方法。

教师在案例讲解中，设计多个环节，有意识地让学生把特定问题放到全局中思考。比如，在将现实问题转换为数学问题时，提出诸如问题边界在哪里、问题边界是否会影响数学模型的构建、数学模型的约束条件是不是反映了问题在全局中的位置等问题，提示学生思考的维度和广度。在案例总结环节，鼓励学生从更多的角度思考已经有答案的问题，突破局部思维的局限，提出解决的方法，数学模型的求解结论应符合更多元的实际场景。在课程报告撰写环节，要求学生将课堂上案例分析采用的数学方法拓展到类似领域，并进行可行性论证和阐述。

三、基于PDCA循环理念的教学实施设计

在以专业应用为导向的研究生数学教学过程中，强调思维能力的训练和培养，强调与专业研究的深度融合。这种教学有别于传统的以经典教材为主导的数学教学方式，需要不断根据学生的反馈，了解学生对知识的理解和能力的变化，适时反思总结教师和学生在“教与学”过程中可优化提升的部分，才能够达到螺旋提升的目标。借鉴全面质量管理PDCA循环的理念，通过Plan（计划）、Do（执行）、Check（检查）和Assess（评估）四个环节的不断循环，持续改进过程和方法。按照PDCA四个阶段设计课内课外相结合的教学任务（如表3所示），以专业案例教学为中心，对每个案例教学进行回溯总结，并形成“教与学”双向反馈模式，评估每一个案例教学的有效性，为教学的持续改进提供依据。

结语

以专业应用为导向是研究生数学教学的核心目的，无论是数学知识和专业案例的针对性选择，还是学生的思维能力训练，都需要相关教学环节的精细化设计，对授课教师的专业素养和数学能力都提出了更高的要求。本文提出通过课前、课中、课后的PDCA循环过程，融入启迪数学思维的过程训练，启发学生构建专业领域数学知识框架，重点强调数学方法的理解和应用分析，以引导学生将数学知识和专业理论研究和实际问题解决建立联系，为后续专业课程及其他相关学科的学习和自主学习打下坚实的基础。