[出处] 教育教学论坛_2022年第6期

彭湘凌 陈单单 刘振林 肖其珍 刘宏亮

[关键词] 课程思政；微积分基本公式；数学历史人文；精神品质

[基金项目] 2020年度湖南省学位与研究生教育改革研究项目“数学专业研究生课程教学改革的探索与实践”（2020JGYB175）；2020年度湖南财经工业职业技术学院教育教学规划课题项目“论高等数学课堂从历史人文与哲学辩证的角度展开课程思政的研究”（202014）

[作者简介] 彭湘凌（1989—），男，湖南衡阳人，硕士，湖南财经工业职业技术学院公共课部助教，主要从事数学教育、微分方程与动力系统研究；刘宏亮（1981—），男，广东湛江人，博士，南华大学数理学院讲师（通信作者），主要从事数学教育、微分方程与动力系统等研究。

[中图分类号] G641 [文献标识码] A [文章编号] 1674-9324（2022）06-0097-04 [收稿日期] 2021-06-22

习近平总书记指出，要加大對学生的认知规律和接受特点的研究，发挥学生主体性作用。要坚持传授性和启发性相统一，注重启发性教育，引导学生发现问题、分析问题、思考问题，在不断启发中让学生水到渠成得出结论。要坚持显性教育和隐性教育相统一，挖掘其他课程和教学方式中蕴含的思想政治教育资源，实现全员全程全方位育人[1]。这为“高等数学”课程的教研教改作出了重要指示。作为高等数学教师不仅要向学生传授高深的数学知识，同时还要充分挖掘高等数学知识中蕴含的数学品质、数学精神和数学文化，与培养新时代大学生优秀精神品质和风貌相呼应，切实履行高等数学教师注重思想政治教学的使命职责，始终围绕“培养什么人、怎样培养人、为谁培养人”这一理念去教学，为培养中国特色社会主义事业合格建设者和可靠接班人，书写好新时代教育的奋进之笔贡献自己的绵薄之力。

一、课程思政的产生与当前“高等数学”课程的相容性

随着信息网络社会的发展，面对西方文化思潮的冲击，对于一些新生事物许多学生还没有形成正确的辨识能力，容易遭受腐朽污浊的思想文化的侵蚀，误导他们的世界观、人生观和价值观，具体表现为国家意识淡薄、民族观念薄弱、忽视我国优秀传统文化、崇拜西方拜金享乐思想等特点。其主要原因是青少年思想政治意识还未与我国的经济社会发展同步，如何实现两者的齐头并进，是当代教育工作者的重大责任。先进的学科知识背后，必伴随着可贵的精神品质。因此，对青少年的思想政治教育不能仅限于思想政治理论课课堂，若本着立德树人的教学目的，充分挖掘其他学科知识中蕴含的思想政治教育元素，并在课堂运用得当，那么学生在享受学科知识教育的同时，又能自然地接受到优秀思想和精神的滋养，不失为一种好的教学理念。而且过去对学生的思想政治教育也主要是由思想政治理论课程担当主力，在其他学科课程中的思想政治教育体现的不够明显。究其原因，既有其他学科课程内容本身教学任务繁重，也有其他学科教师教学本位主义思想作祟等缘故。再因，思想政治理论课程以丰富的经典理论、历史经验和社会现实为主体，若在课堂讲解过程中，与学生的个人生活实践联系不够密切，或教学方式比较单一，则容易导致学生对思想政治知识的理解不够透彻，学习的主动性不强。为解决这一困境，应在对学生思想政治教育方法上开辟新的疆土，不局限于思想政治理论课课堂，而在其他的学科课堂中融入思想政治教育，是其他学科教师应承担的思想政治教育任务，真正肩负起培养社会主义合格建设者和接班人的使命。因此，如何在其他学科课堂中有效地开展思想政治教育，成为当代教育的一个重要研究课题。2014年，上海市教育领域率先提出课程思政的概念[2]。它是将思想政治教育融入所有课程教学的所有环节的一种新的教育理念，实现与思想政治理论课程产生同向同行的协同效应，使所有课程达到润物无声的立德树人的教育目标。这一概念的提出，为其他学科的思想政治教学带来了理论曙光，并迅速得到了教育部及有关领导的关注和重视。目前，课程思政的教学观念日益深入人心，并掀起了一股关于课程思政教学改革的时代热潮。

随着课程思政的全面开展，“高等数学”课程教学改革势必要跟进时代潮流，承担立德树人的职责使命。简单来说，“高等数学”课程是一门研究“数”与“形”的基础学科，所讨论的都是高度抽象与概括的问题。伟大的思想家马克思指出，一种科学只有在成功地运用数学时，才算达到了真正完善的地步[3]。可见数学是科学的基础，具有广泛的通用性和先进性，在它的历史发展过程中，必具备丰富多彩、激人奋进的人文思政内涵。但这一点往往不被大多数人所理解，对数学的学习普遍停留在代数计算和几何认识阶段，对数学背后的人文思想不甚了解，一味地忽视数学方面的人文素质培养，是数学教育的一大浪费。学生普遍疲于课本教材严格的公式推演和计算，关注考试的知识范围和答案的对错，有时还被严谨的推导证明所吓倒，长此以往，容易对数学产生误解，过分地否定自己学习数学的能力，认为数学是少数人学的，总是在反复考查计算能力，甚至出现数学无用论的错误想法。这主要是由于学生对数学是片面认识，其实大多数学生在学习时，把高等数学只当作其他学科的计算工具，被书中的练习计算所累，找不到其中的学习乐趣，也不愿意多花精力去学习、去理解和去联想数学知识背后的奥妙，导致学习兴趣不高，主动性不强，成绩不理想，最后对数学产生恐惧厌恶情绪。作为高等数学教师，如何提升学生学习数学的兴趣，提高对数学的认识，理解高等数学的重要性，一直是一个重要的课题。为解决这一课题，有许多教育工作者在“高等数学”课程教学信息化方面寻求突破，建立了许多网络学习资源平台，拓展学生的学习渠道和学习方式，对数学的教学工作起到了很大的促进作用。但学习内容并未有创新，只是教学形式的创新，学生还是被动式的学习，对数学没有太多思考。成绩好的学生普遍还是拼命学习数学计算，把自己训练成“解题机器”，从未感受到真正的数学文化内涵，也并未提升对“高等数学”课程重要性的认识，数学学习还是只为应付考试的狭隘思想，这有违我们真正的数学教育目的。对张奠宙教授“数学文化必须走进课堂，在实际数学教学中，使学生在学习数学的过程中真正受到文化感染，产生文化共鸣，体会数学的品味与世俗的人情味”[4]这句话进行思考，将极大丰富数学知识教育的内涵，其实数学教育不只是培养学生的逻辑思维能力和计算能力，学生若能在数学学习过程中，接触一些数学文化，了解一些数学公式的历史由来，领悟一些数学家的励志故事，感受一些他们的精神品质，那么数学知识将不再那么枯燥单调，数学知识的趣味性也会增加。这不仅能激发学生学习数学的兴趣，也能培养学生优秀的人格品质，这实际就是数学课堂的思想政治教育，将实现数学知识、数学人文和思想政治教育三驾马车并驾齐驱。因此，这样的数学课堂完全符合当前课程思政的内涵，能够做到与思想政治理论课程的同向同行，达到立德树人的教育目标。

二、从历史人文角度挖掘“高等数学”课程思政元素

1.由微积分基本公式的来龙去脉，引出科学家久久为功、持之以恒的精神。恩格斯曾这样评价：“在一切理论成就中，未有像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了，如果在某个地方我们看到人类精神的纯粹的和唯一的功绩，那就正是在这里。”[5]顺着恩格斯对微积分的评价，可以给学生讲授微积分的历史，既有利于学生对数学科学史的了解，学习科学家的创新求索精神，激发学生的数学学习兴趣，同时也有利于学生了解数学发展的来龙去脉，明白数学学习的价值和意义。对于微积分的思想研究中外古已有之，我国魏晋时期数学家刘徽在《九章算术·圆田术》注中提出：“割之弥细，所失弥少”；南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异”；古希腊的欧多克索斯的“穷竭法”，以及后来的数学家、哲学家、物理学家阿基米德的“逼近法”等，从现在课本的知识结构来看，他们都是在没有现代极限理论的情况下，提出了一种直接、朴素的数学方法，这已是微积分思想的雏形，他们的工作具有前瞻性和启发性，有待后世去完善和发展。正因如此，大学生要努力学习当代数学知识，理解书本基本公式和定理的原理，因为这些也是一代代科学家通过不断创新和积累得到的成果，但有些并不一定是终极性的结果，在熟练掌握这些經典的理论基础知识后，可能也会在一定程度上激发学生某些启发性思考，学生可作数学方向上的延伸研究，亦可作实际应用推广上的探究。如今教科书上的微积分基本公式为：

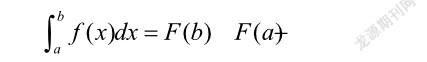
其又名“牛顿-莱布尼茨公式”，因为它的产生以17世纪牛顿和莱布尼茨的工作为标志。17世纪，为了满足社会实践生产和科技发展的需求，微积分理论的诞生可谓是呼应时代的召唤，当时对数学家提出了四个主要问题[6]：（1）求已知位移与时间的函数，求任意时刻速度和加速度的问题；（2）物体运动轨迹上任一点的切线问题；（3）求函数最大值和最小值问题；（4）求曲线围成的面积问题。其中（1）（2）（3）可以说是微分问题的来源，（4）是积分问题的来源，牛顿和莱布尼茨正是基于这些问题的思考和前人的成果，提出了开创性的方法，将积分与微分统一起来，两者存在互逆的关系，建立了微积分基本公式，解决了困扰学界一千多年的问题。这是令人惊叹的功绩，惊叹之余，本着唯物主义思想，学生应该要思考他们是如何拥有这创世之举的？牛顿是这样告诉大家的：我并没有什么方法，只不过对于一件事情，总是花很长的时间热心去思考罢了。首先，这是一种伟人的谦逊，值得我们学习与敬仰。其次，是一种凡人的执着、勤奋和思考，正是思想政治教育所提倡的那种孜孜不倦、久久为功、持之以恒的科学研究精神，这正是我们当代大学生需要迫切学习的。往往我们有不少学生，碰到数学难题，就产生畏难情绪，不愿意思考，急切否定自己，这种情况先不讨论学生对知识的掌握，仅在精神品质上就输人一局。我们“高等数学”课程教育，既有知识传授的功能，更有精神品质培养的功能，且至关重要，无可替代。经历“高等数学”课程学习的“磨炼”，有助于学生迎难而上精神品质的培养，以这样学习精神和态度去面对自己的人生，必能成就一番事业。

2.由微积分基本公式的曲折发展，引出科学家不惧批判，勇于拼搏的精神。微积分基本公式诞生之后，以摧枯拉朽之势解决了物理界许多问题，应用微积分得到的任何成果都是正确的。但尴尬的是，微积分的成立证明在当时却被认为是荒唐的。牛顿和莱布尼茨都给不出微积分基本公式的严格证明，因为缺乏极限理论，对某些关键的环节，只能给予个人主观的说明。这好比牛顿和莱布尼茨是微积分基本公式这个天才“孩子”的“接生婆”，但没办法给他开出合法出生证明，这样的情况，肯定会给他们二人的身份招来众多的非议。是为了个人的名誉清白而停止研究，还是为了科学进步，继续研究，饱受非议呢？牛顿和莱布尼茨都选择了后者。1684年，莱布尼茨发表了《一种求极大、极小值与切线的新方法》的论文，定义了微分的符号及其四则运算；1687年，牛顿发表了《自然哲学的数学原理》的科学名著，里面记载了流数术的方法[7]。虽然一起开启了微积分的数学时代，但二人的理论都有一个缺陷，就是无法对无穷小量进行严格分析，但微积分证明的关键环节却使用了它。如此伟大的一个公式，里面却有一个这么大的漏洞，众人对于他们的攻讦可想而知。意大利贝克莱大主教评价微积分公式是：依靠双重错误得到了不科学但却正确的结果，并嘲笑那个无穷小量为“已死量的幽灵”[8]。贝克莱主教的批评是有道理的，也是切中要害，数学界知名的“贝克莱悖论”就是这样来的，第二次数学危机也是由此产生的。在数学课堂上，这些知识可以帮助学生树立正确的科学历史发展观，科学的道路上，不是一帆风顺的，不时会有一些意想不到的障碍，但只要是真理，最终还是会在曲折反复中前进。当代大学生要勇于树立自己崇高的理想，不能因为害怕一时失败所遭受的非议，就降低自己的品位，相信自己具备“志不求易者成，事不避难者进”的本领。牛顿和莱布尼茨在没搞清楚无穷小量到底是“0”还不是“0”的情况下，提出微积分公式的惊世之举，需要莫大的勇气，即使他们最终都没有修补那个缺陷，但他们取得的成绩是斐然的。后来涌现出的欧拉、狄利克雷、黎曼、达朗贝尔等一大批的数学家，他们沿着牛顿和莱布尼茨的足迹前进，直到柯西和魏尔斯特拉斯建立严格的极限定义，这个缺陷才终于解决。给学生讲述一代又一代数学家的伟绩，并不是要描述数学家功绩的编年史，更多的是给学生讲解科学家们为一个公式执着追求的奋斗史，帮助学生在学习数学知识的同时，树立勇于拼搏奋斗的精神。

结语

学生学习“高等数学”课程的重要性是毋庸置疑的，但学习“高等数学”的困难亦是不可避免的。掌握高深的数学知识，势必要付出勤奋努力的代价。而在不懈奋斗的学习过程中，挖掘其中的乐趣，了解数学知识的历史来源和先进人物，激发自己，勉励自己，不失为一种好的方法。正所谓“欲知大道，必先为史”，正是如此。数学历史必将是数学课程思政的源泉。在“微积分基本公式”的课堂上，通过对微积分基本公式人文历史的探索，激发学生兴趣，让学生了解数学公式定理发展的传奇故事。回顾历史，瞻仰伟人，以感性的情怀学习数学知识，以理性的思维完成学习任务，既摆脱了数学公式的枯燥乏味，也为数学学习增加了不竭动力，同时培养了学生高尚情操，使“高等数学”课堂不仅教学生数学知识，也教学生诗与远方。